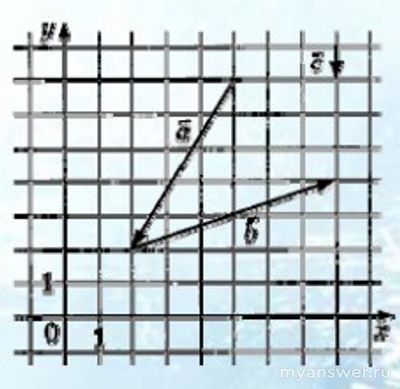
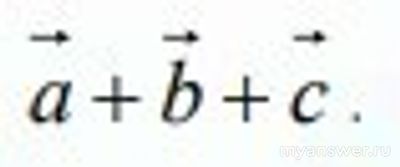На координатной плоскости изображены векторы a, b и c. Как найти а+b+с?
Ответы (2)
Искомая длина равняется корню квадратному из суммы квадратов координат вектора, получающегося в результате суммирования векторов a, b и с.
По рисунку из условий задачи определяем координат трёх суммируемых векторов:
a(-3;-5),
b(6;2),
с(0;-1.
Координаты вектора, являющегося суммой трёх этих векторов:
(-3+6+0;-5+2+(-1)) = (3;-4).
Искомая длина этого вектора:
(3^2+(-4)^2)^0,5 = (9+16)^0,5 = 5.
Ответ: 5.
Стандартный метод решения задач на векторы в координатной плоскости состоит в следующем.
1) Определяем координаты векторов по изображению (как разность координат конца и начала).
2) Используем формулы для суммы (разности, произведения на число, скалярного произведения, длины вектора и т.д.) векторов через их координаты.
В нашем случае координаты векторов такие: а{-3;-5}, b{6;5}, c{0;-1}.
Теперь воспользуемся формулой суммы векторов.
а+b+с = {-3+6+0;-5+6+(-1} = {3;0}. Длина вектора а+b+с равна корню квадратному из суммы квадратов координат то есть V(3^2+0^2)=V9=3. Ответ: 3.