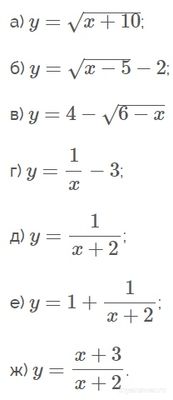y = √x — это график квадратного корня, начинающийся в точке (0, 0) и возрастающий вправо.

y = 1/x — это гипербола с асимптотами x = 0 и y = 0.

а) y = √x + 10

Преобразование: Сдвиг графика y = √x на 10 единиц вверх вдоль оси y.

Описание: График будет выглядеть как y = √x, но начинаться будет в точке (0, 10).

б) y = √x - 5 - 2

Преобразования:

Сдвиг графика y = √x на 5 единиц вправо вдоль оси x (замена x на x - 5).

Сдвиг полученного графика на 2 единицы вниз вдоль оси y.

Описание: График будет выглядеть как y = √x, но начинаться будет в точке (5, -2).

в) y = 4 - √6 - x

Преобразования:

Замена x на -x, то есть отражение графика y = √x относительно оси y.

Сдвиг графика y = √(-x) на 6 единиц вправо вдоль оси x (замена x на x-6). Получаем y=√-(x-6)=√6-x

Отражение графика y = √6 - x относительно оси x (замена y на -y). Получаем y=-√6-x.

Сдвиг полученного графика y = -√6 - x на 4 единицы вверх вдоль оси y.

Описание: График будет зеркальным отражением y = √x относительно оси x и оси y. Он будет убывать, начинаться в точке (6, 4) и будет идти влево.

г) y = 1/x - 3

Преобразование: Сдвиг графика y = 1/x на 3 единицы вниз вдоль оси y.

Описание: График будет выглядеть как y = 1/x, но с горизонтальной асимптотой y = -3.

д) y = 1/(x + 2)

Преобразование: Сдвиг графика y = 1/x на 2 единицы влево вдоль оси x.

Описание: График будет выглядеть как y = 1/x, но с вертикальной асимптотой x = -2.

е) y = 1 + 1/(x + 2)

Преобразования:

Сдвиг графика y = 1/x на 2 единицы влево вдоль оси x.

Сдвиг полученного графика на 1 единицу вверх вдоль оси y.

Описание: График будет выглядеть как y = 1/x, с вертикальной асимптотой x = -2 и горизонтальной асимптотой y = 1.

ж) y = (x + 3) / (x + 2)

Преобразование: Чтобы увидеть преобразования, разделим (x + 3) на (x + 2). Получим:

y = (x + 2 + 1) / (x + 2) = (x+2)/(x+2) + 1/(x+2) = 1 + 1/(x+2)

Описание: Как видно, это то же самое преобразование, что и для примера “е”. График будет выглядеть как y = 1/x, с вертикальной асимптотой x = -2 и горизонтальной асимптотой y = 1.