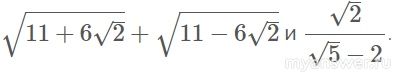а)√29 и 5

5= √25 , т.к. 29>25 , то √29 > √25

√29 > 5

б) √17 + √33 и √79

в) √11 + √13 и 7

г) √19 - 3√2 и √21 - 2√5

Внесем сомножители 3 и 2 в подкоренные выражения

√19 - √18 √21 - √20

Умножим и разделим каждое выражение на два одинаковых числа:

√19 - √18 )*(√19 + √18 )/ (√19 + √18 ) = (19-18)/ (√19 + √18 ) = 1/ (√19 + √18 )

( √21 - √20)*( √21 + √20)/ (√21 + √20) = 1/ (√21 + √20)

таким образом, можно сравнить две дроби: больше та, знаменатель которой меньше

(√19 + √18 )< (√21 + √20), значит

√19 - 3√2 > √21 - 2√5

д)

√(11+6√2) + √(11-6√2) и √2/(√5-2)