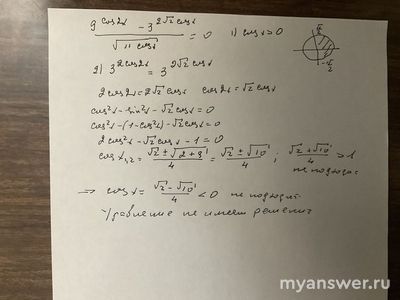Как решить пункты а и б: 9^(cos2x) - 3^(2√2 cosx)...( см.)?
Ответы (2)
Во-первых, смотрим на знаменатель, который не должен равняться 0.
cos x ≠ 0
x ≠ pi/2 + pi*k, k Є Z
Во-вторых, числитель должен равняться 0.
9^(cos 2x) - 3^(2√2*cos x) = 0
Вспоминаем свойство степеней при возведении в степень:
a^(bc) = (a^b)^c
И формулу косинуса двойного угла:
cos 2a = 2cos^2 a - 1
Поэтому
9^(cos 2x) = (3^2)^(cos 2x) = 3^(2cos 2x) = 3^(4cos^2 x - 2)
3^(4cos^2 x - 2) - 3^(2√2*cos x) = 0
3^(4cos^2 x - 2) = 3^(2√2*cos x)
Если степени равны и основания одинаковы, то и показатели равны:
4cos^2 x - 2 = 2√2*cos x
Делаем замену t = cos x, получаем квадратное уравнение:
4t^2 - 2√2*t - 2 = 0
Делим всё на 2:
2t^2 - √2*t - 1 = 0
D = 2 - 4*2(-1) = 2 + 8 = 10
t1 = (√2 - √10)/2
t2 = (√2 + √10)/2
Обратная замена:
cos x1 = (√2 - √10)/2
x1 = +-arccos((√2 - √10)/2) + 2pi*k, k Є Z
cos x2 = (√2 + √10)/2
x2 = +-arccos((√2 + √10)/2) + 2pi*k, k Є Z
Очевидно, что ни при каком из этих x не будет cos x = 0, поэтому это и есть ответ.