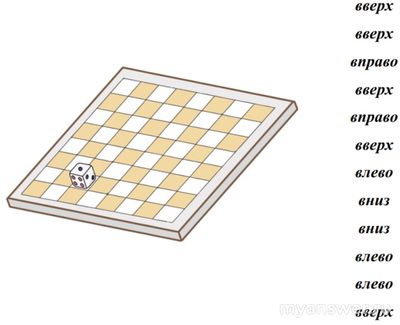
Задача. Верно ли, что исполнитель «Кубер» не встанет на ту же грань?
Исполнитель «Кубер» передвигается по клеточному полю с помощью команд:
направо – перекатывается на грань в соседнюю клетку
справа;
налево – перекатывается на грань в соседнюю клетку
слева;
вверх – перекатывается на грань в соседнюю клетку
сверху;
вниз – перекатывается на грань в соседнюю клетку снизу.
Верно ли, что, выполнив команды, представленные ниже, исполнитель «Кубер» не встанет на ту же грань, что и в начале? Исходная позиция представлена на картинке.
Ответы (3)
В условии требуется именно та же грань внизу. Обозначим её "Х".
Заметим, что если искомая грань вверху или внизу, то любая команда меняет её положение. А если искомая грань с боку, то положение будет меняться если грань с того боку екда команда или с противоположного. Иначе изменения положения нет.
Таким образом две команды подряд "вверх" поменяют положение Х на верхнее.
Потом команда "вправо" переведет Х справа.
Далее команда "вверх" никак не меняет положения
А команда "вправо" снова переведет Х в нижнее положение.
Снова "вверх" переведет в боковое положение Х (он будет повернут на нас)
И теперь команда "влево" никак не изменит это положение.
А вот две команды "вниз" переведут Х в противоположное и он будет находится с тыльной стороны.
И снова команда "влево" никак не изменит положения. И 2 подряд такие команды тоже.
И наконец последняя команда "вверх" переведет грань Х в нижнее положение.
Исполнитель встал на ту же грань.
Ответ: не верно, что после этих команд не встанет на эту же грань.
Чтобы исполнитель "Кубер" встал на прежнюю грань, количество команд "вверх" должно быть равно количеству команд "вниз", или одно из этих количеств должно быть больше другого количества на число, кратное числу четыре. Это же одновременно касается и другой пары команд - "влево" и "вправо".
По факту имеется такое количество команд:
"вверх" = 5 команд,
"вниз" = 2 команды,
"влево" = 3 команды,
"вправо" = 2 команды.
Как отсюда видно, исполнитель "Кубер" не встанет в итоге на свою прежнюю грань.
Вообще говоря, тут важно не просто сколько поступило команд "вверх" или "вниз" или ещё каких-то, а важна и последовательность команд. То, что тут происходит, описывается в терминах теории групп, когда каждая операция есть элемент группы. А там операция умножения, то есть применение двух последовательных преобразований (переворот на соседнюю грань) не является коммутативной.
Поэтому тут можно тупо расписать, что будет с кубиком после каждой операции... но лучше нарисовать. Памятуя при этом, что сумма очков на противоположных гранях всегда равна 7.
Ну и видим, что после всех операций кубик вернулся в исходное положение.