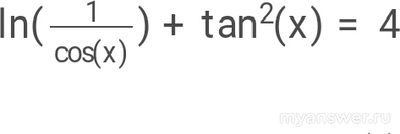ln (1/cos x) + tg^2 x = 4

Область определения:

{ 1/cos x > 0

{ cos x ≠ 0

Получаем:

cos x > 0

x Є (-pi/2 + 2pi*k; pi/2 + 2pi*k), k Є Z

Решаем уравнение.

Прибавим 1 слева и справа:

ln (1/cos x) + (1 + tg^2 x) = 1 + 4

Как известно, 1 + tg^2 x = 1 + sin^2 x/cos^2 x = (cos^2 x + sin^2 x)/cos^2 x = 1/cos^2 x

ln (1/cos x) + 1/cos^2 x = 5

Замена 1/cos x = t. Так как cos x > 0, то cos x Є (0; 1], тогда t Є [1; +oo)

ln t + t^2 = 5

ln t + t^2 - 5 = 0

Решать это аналитически очень трудно, графически намного проще.

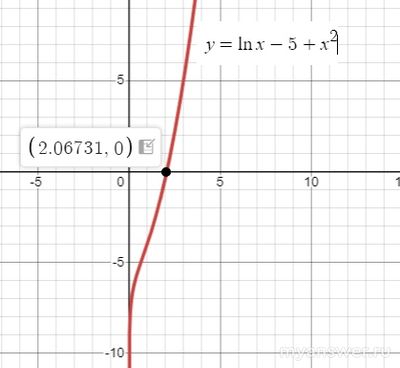
На рисунке показан график функции y = ln x + x^2 - 5.

Извините, на графике пришлось использовать переменную x, а не t.

График имеет одно пересечение с осью Ox в точке x0 ≈ 2,06731

Получаем:

t = 1/cos x = 2,06731 ≈ 2

cos x ≈ 1/2

x ≈ +-pi/3 + 2pi*n, n Є Z