Сколько решений имеет уравнение |x^2-7|x|+6=a|, при a принадлеж. (0;6)?
Ответы (2)
А зачем внешний модуль? Он не несет никакой смысловой нагрузки и только засоряет уравнение. Или вы списать уравнение правильно не смогли и знаки модуля стояли иначе?
Но решим в таком виде.
Решим графически. Пусть t = |x|
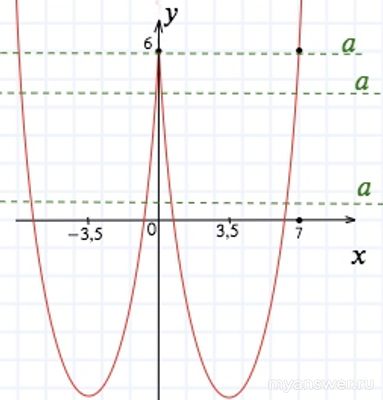
Видим y = t² - 7t + 6 - квадратное уравнение. Графиком которого будет парабола.
Ветви направленны вверх. Вершина в точке t = 7/2 = 3,5
y(3,5) < 0
y(0) = 6 - ось Oy пересечется в точке (0; 6) (очень удачно)
И y(|x|)- будет просто симметричным графиком положительной части y(x) относительно оси Oy
Строим схематично параболу, её симметричную часть в отрицательной части и проводим прямые y = a от 0 до 6
Видим что везде будет 4 точки пересечения графика с прямой
Соответсвенно
Ответ: 4 решения
Но в условии этого не указано, а указан внешний модуль на все выражение (он бессмысленен в таком виде), но что поделаешь. Не стоит гадать как оно должно было быть, а решение согласно указанному заданию в вопросе.
Все-таки я решил выложить решение уравнения:
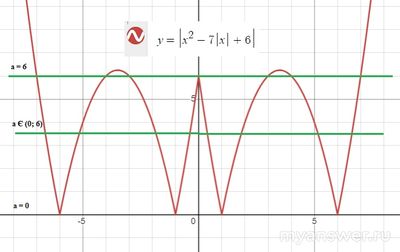
|x^2 - 7|x| + 6| = a при a Є (0; 6)
Решение тоже графическое, решать такое аналитически очень муторно.
Как видим, при a = 0 уравнение имеет 4 корня, при a = 6 оно имеет 7 корней.
А при a Є (0; 6) это уравнение имеет 8 корней.
Две параболы с ветвями вниз имеют вершины в точках (-3,5; 6,25) и (3,5; 6,25).