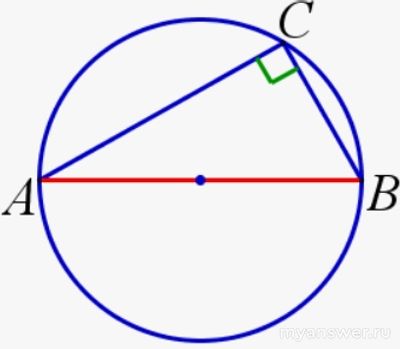
Как решить: На окружности лежат 50 точек?
На окружности лежат 50 точек. Выберем все тройки точек, которые образуют прямоугольный треугольник. Сколько таких троек может оказаться?
- таких троек может оказаться 1920
- таких троек может оказаться 1000
- таких троек может оказаться 432
- таких троек может оказаться 420
Дайте обоснование такого выбора.
Ответы (4)
Ну, вообще, условие какое-то мутное: каким образом расположены эти 50 точек по окружности, да и их количество как-то не ровно делит круг, по 7,2°, при условии, что между точками должны быть одинаковые интервалы.
Но условия придумываем не мы ;-)
Если всё-таки интервалы между точками должны быть одинаковыми, то их все можно разделить на 25 пар, лежащих друг напротив друга и являющихся, скажем так, концами диаметров. На каждом таком диаметре можно построить 50 - 2 = 48 прямоугольных треугольника.
В общем, у меня получается несколько отличающийся, от предложенных вами, вариант, не самый большой и не самый маленький:
25 * 48 = 1200
Если нам необходим вписанный в окружность прямоугольный треугольник, то прямой угол всегда должен опираться на диаметр.
Возьмём пару диаметрально-противоположных точек, В и А.
А точка С может перемещаться по окружности в черт знает скольких положениях.
Из 50 точек остается еще 48 вариантов.
И это только по первой паре А и Б.
Потом берем другую пару, Б и С, - это еще 48 вариантов.
А всего из 50 точек можно составить 25 пар.
25 пар дадут по 48 вариантов - это (считаю на калькуляторе), получается 1200 вариантов.
Только одно условие, все точки НЕ лежат на одной полуокружности. А хотя бы равномерно как-то распределены по всей окружности.
Иначе говоря, необходимо дополнительное условие. чтобы всякой точке была в пару диаметрально противоположная.
Понятно, что если все точки лежат по одну сторону от диаметра, то таких троек будет 0.
Вообще, 0 будет и если ни одна пара точек не лежит на диаметре.
Прямой угол обязан опираться на диаметр.
Найдём максимальное количество таких троек.
Если две точки лежат на диаметре, остальные 48 образуют с ними ту самую тройку.
Максимальное число таких троек мы получим, если все 50 точек будут образовывать пары, лежащие на одном диаметре.
Тогда у нас будет 25 диаметров, на каждом из которых по 48 прямых углов.
25*48 = 1200 - максимально возможное число таких троек при идеальных условиях
В любом случае, число таких троек будет кратно 48.
Потому что тут - или всё или ничего.
Сколько у нас есть пар точек, образующих диаметр, столько и наборов треугольников по 48 штук автоматом мы получаем.
таких троек не может оказаться 1920, потому что максимум мы нашли, и это 1200.
таких троек не может оказаться 1000, потому что 1000 не делится на 48
таких троек может оказаться 432, если 9 пар точек лежат на диаметрах
таких троек не может оказаться 420, ибо 420 не делится на 48 нацело.
Из предложенных вариантов только 432 годится
Треугольник, полученный соединением трёх точек, лежащих на окружности, будет прямоугольным, если две его точки будут диаметрально противоположными.
Каждая пара таких диаметрально расположенных точек даст 48 различных треугольников.
Теперь, к вариантам ответов.
Почему-то, число 1920 указано дважды. Ну, да, ладно.
И так, нацело на число 48 делятся только два из предложенных чисел:
1920 / 48 = 40,
432 / 48 = 9.
Ответ на задачу: Таких троек может быть 9, или 40 штук.