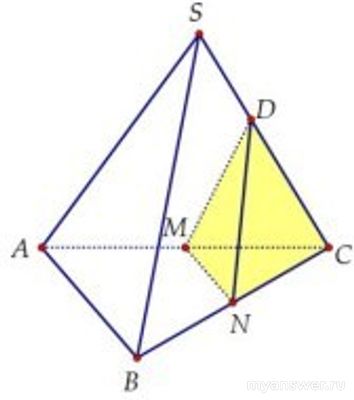
Как решить: Объем треугольной пирамиды SABC равен 100. Точка D лежит...?
Как решить задачу (ЕГЭ математика)?
Объем треугольной пирамиды SABC равен 100. Точка D лежит на ребре SC и делит его в отношении 2:3, считая от вершины S. Отрезок MN – средняя линия треугольника АВС, параллельная стороне АВ. Найдите объем пирамиды DMNC.
(Ларин, тренировочный вариант 489)
Ответы (1)
Решение:
В подобных треугольниках стороны, лежащих против равных углов, пропорциональны.
Высоты пирамид SABC и DMNC вместе с ребрами SC и DC
являются гипотенузами подобных треугольников, в которых гипотенузы соотносятся
в отношении 2:3 , значит и высоты пирамид также в отношении 2:3.
Площадь основания большой пирамиды S1 = 1/2*AC*BC*sinACB
Площадь основания малой пирамиды S2 = 1/2*MC*NC*sinACB
Т.к. по условию AC = 2*MC, BC = 2*NC, то
S1 = 4*S2.
Т.к. объем пирамиды равен трети произведения площади основания на высоту,
то соотношение объемов пирамид V1 и V2
V1:V2 = 4*3/2 : 1 = 6 : 1.
V1 = 100, тогда V2 = 100/6 = 16.(6) = 16.7
Ответ: объем пирамиды DMNC = 16.7
ВКонтакте