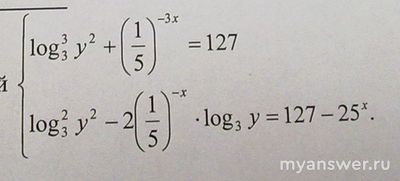Как решить систему уравнений log^3 3 y^2+(1/5)-3x=127...?
Система:log^3 3 y^2+(1/5)^(-3x)=127
log^2 3 y^2-2(1/5)^(-x)*log3 y=127-25^x
Ответы (2)
Итак, данное задание является ( наверное...) повышенной сложности, но напишу, то как я попытался её решить. Во- первых, заметим, что (1/5)^(-3x), (1/5)^(-x) и 25^x имеют нечто общее. Теперь преобразуем 25^x= (1/5)^(-2x) и заменим, пожалуй, (1/5)^(-x)=t. А также увидим похожесть log^3 3 y^2, log^3 2 y^2 и log3 y, заменив log3 y = m>0. Теперь напишем , что у нас получилось:
2m³ + t³ = 127
И
2m²- 2tm + t² = 127
Ура, у нас получилось, что справа написано 127, а значит приравняем левые части, перенеся всё в одну сторону.
2m³+t³-2m²+2tm-t²= 0
2m²(m−1)+2tm+t²(t−1)=0
2•log3y•(log3y-1)+2•log3y•(1/5)^(-x) + (1/5)^(-2x)•( (1/5)^(-x)-1)=0
Таким образом, видимо что-то есть в условии ( что вы не написали), так как почему-то не решается дальше. Прошу "htf-msk", "epimkin", "Mefody66", "ОлегТ" или других посмотреть более внимательнее на данную систему и моё предполагаемое решение ( вернее его ход), может быть дополнить, решить эту странную систему.
P.S конечно я не решил до конца данное уравнение, но была уверенность, что я смогу решить, а когда числа не подошли, удалять как-то не хотелось( а так, я думаю, что если как-нибудь опять сделать замену, то с радостью ( или нет...) можно решить замечательной громоздкой формулой Кардано ...
Тут действительно напрашивается замена переменных.
Обозначим 2log₃y = u, 5^x = v. Тогда систему можно переписать в таком виде:
u³ + v³ = 127
u² -uv + v² = 127
Теперь вспоминаем формулу суммы кубов: она раскладывается на произведение суммы оснований на неполный квадрат разности оснований. То есть
(u+v)(u² -uv + v²) = 127
(u² -uv + v²) = 127
Откуда сразу следует, что u+v=1.
Значит, теперь имеем такое:
u+v=1
u² -uv + v² = 127
Последнее уравнение перепишем в таком виде:
u² + 2uv + v² -3uv = 127
или
(u+v)² - 3uv = 127
Так как мы уже знаем, что такое u+v, это уравнение превращается в вот что:
-3uv = 126, uv = -42.
В итоге наша система упростилась до безобразия:
u+v = 1
uv = -42
Всё, дальше элементарно. Обратите внимание, что в этом виде система симметрична, то есть корни "взаимозаменяемы" - с тем ограничением, что v>0 (это степень пятёрки). Так что u = -6, v = 7.
И вся любовь.
ВКонтакте