Периметр треугольника ABC равен 2√85 + 26 см или примерно 44,44 см.

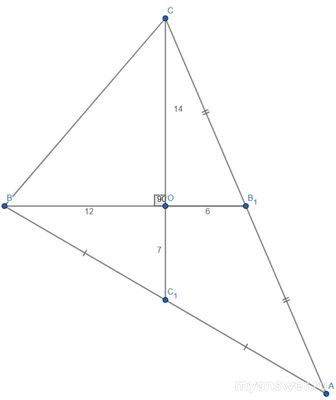
Медианы делятся точкой их пересечения в отношении 2:1 от вершины. Отсюда BO=18*2/3=12, OB1=18*1/3=6, CO=21*2/3=14, OC1=21*1/3=7.

Треугольник BOC прямоугольный, длины катетов BO и CO нам известны, найдём по теореме Пифагора длину гипотенузы: BC = √(BO²+CO²)=√(144+196)=√(340)=2√(85)

Треугольники BOC1 и COB1 также прямоугольные, и длины их катетов нам также известны. Найдём длины гипотенуз:

BC1=√(BO²+OC1²)=√(144+49)=√(193)

B1C=√(CO²+OB1²)=√(196+36)=√(232)=2√(58)

Теперь найдём длины сторон:

AB=2BC1=2√(193)

AC=2B1c=4√(58)

И, наконец, сложим длины сторон и получим периметр:

P=AB+AC+BC=2√(85)+√(193)+2√(58)